Ján Mináč
Here is a nice surprise below, and here is the related link:
 ♦ Here is another nice surprise in the form of a Western News article concerning the above event.
♦ Here is another nice surprise in the form of a Western News article concerning the above event.
♦ Here is my short CV (updated February 2025).
Workshop on Galois Cohomology and Massey Products: A conference in honour of Ján Mináč's 71st birthday, June 13 - 16, 2024, University of Ottawa. Organizers: Stefan Gille (University of Alberta), Luisa Liboni (Western University), Kirill Zaynullin (University of Ottawa). Also supported by The Fields Institute for Research in Mathematical Sciences and the Pacific Institute for the Mathematical Sciences.
This was a wonderful conference! I am extremely grateful to the organizers and to all of the participants at this conference. There were some really fascinating and enjoyable talks delivered, as well as a wonderful exchange of ideas and fruitful discussions.

And here is a nice surprise event which took place during this conference.


(Left to right: Marieke Mur, Ján Mináč, Lyle Muller, Alan Shepard, Fred Longstaffe.)
Launch of the Western Academy for Advanced Research, Western University, September 15, 2022
I feel very grateful and privileged to have been chosen as an Inaugural Fellow 2022-23 in the Western Academy for Advanced Research, together with Professors Lyle Muller and Marieke Mur, of our "Theme", computational neuroscience. This is a great opportunity and privilege to work with our wonderful collaborators, students, and postdoctoral fellows on this exciting research.
Dr. Maria Chudnovsky
The Western Academy for Advanced Research - Exciting Events, February 6 - 10, 2023 with Western Academy Visiting Fellow, Dr. Maria Chudnovsky (Princeton), Dr. Sophie Spirkl (Waterloo), and Dr. Logan Crew (Waterloo)
The Western Academy for Advanced Research, in collaboration with the Department of Mathematics, welcomed Western Academy Visiting Fellow, Dr. Maria Chudnovsky (Princeton) to Western University, February 6 - 10, 2023.
Dr. Maria Chudnovsky is one of the world's leading experts in graph theory and was honoured with a MacArthur Fellowship for her considerable contributions to the field.
On February 7, Dr. Chudnovsky delivered a wonderful talk on "Induced subgraphs and tree decompositions." This talk relates to her work with the "Mathematics of Neural Networks," a year-long interdisciplinary project led by Western Academy Fellow, Dr. Lyle Muller (Mathematics) and Western Academy Fellows, Dr. Ján Mináč (Mathematics) and Dr. Marieke Mur (Psychology).
For more information about Dr. Chudnovsky's research and work with the "Mathematics of Neural Networks" project, please see the Western Academy website.
On February 9, the Association for Women in Mathematics presented "A Coffee Hour with Dr. Maria Chudnovsky." This was an extremely inspiring event which generated lively and interesting discussions.
Dr. Chudnovsky was joined by two awesome young mathematicians; Dr. Sophie Spirkl and Dr. Logan Crew of the University of Waterloo's Department of Combinatorics and Optimization.

Working with Maria Chudnovsky, Sophie Spirkl and Logan Crew has been and continues to be very exciting and stimulating! We are looking forward to further collaboration in our research work together.
Short C.V. (updated August 1, 2024)
Professor Lyle E. Muller and the Muller Lab. I treasure my collaboration with Professor Lyle E. Muller, and our joint co-supervision of some extremely talented, dedicated, and inspiring students and postdoctoral fellows.
Tung Tho Nguyen. Tung Tho Nguyen is an unusually talented, hard working, and creative postdoctoral fellow. He is one awesome example of the exceptional level of our postdoctoral fellows.
Here below is a large part of our awesome interdisciplinary research team together with President Alan Shepard and the Director of the Western Academy for Advanced Research, and Distinguished Professor, Fred Longstaffe; together with Professor Keith Porter and another Western Fellow of the Western Academy for Advanced Research Theme which began in January 2023.
(From left to right, front row: Mohamad Ali Kesserman, Ján Mináč, Maryam H. Mofrad, Marieke Mur, Aishwarya Pathak, Priya Bucha Jain, Alexandra Busch, Roberto Budzinski, Gabriel Benigno, Esther Yartey. Second row: Loxian Kasa, Erwan Martin, Lyle Muller, Alan Shepard, Fred Longstaffe, Lesley Rigg, Keith Porter, and a person to be identified in the near future.)

Canadian Mathematical Society 2019 Second Inaugural Class of Fellows
This photo is a subset of the total of 11 CMS 2019 Second Inaugural Class of Fellows who attended the CMS Winter Meeting Awards Banquet in Toronto on December 8, 2019. The 11 CMS 2019 Second Inaugural Class of Fellows: Louigi Addario-Berry (McGill), James G. Arthur (Toronto), Karl Dilcher (Dalhousie), George A. Elliott (Toronto), Joel Feldman (UBC), Neal Madras (York), Javad Mashreghi (Laval), Ján Mináč (Western), Monica Nevins (Ottawa), Bruce L. R. Shawyer (retired), and Cameron L. Stewart (Waterloo). What a wonderful privilege it is to be learning from and inspired by my 2019 CMS Fellow colleagues.

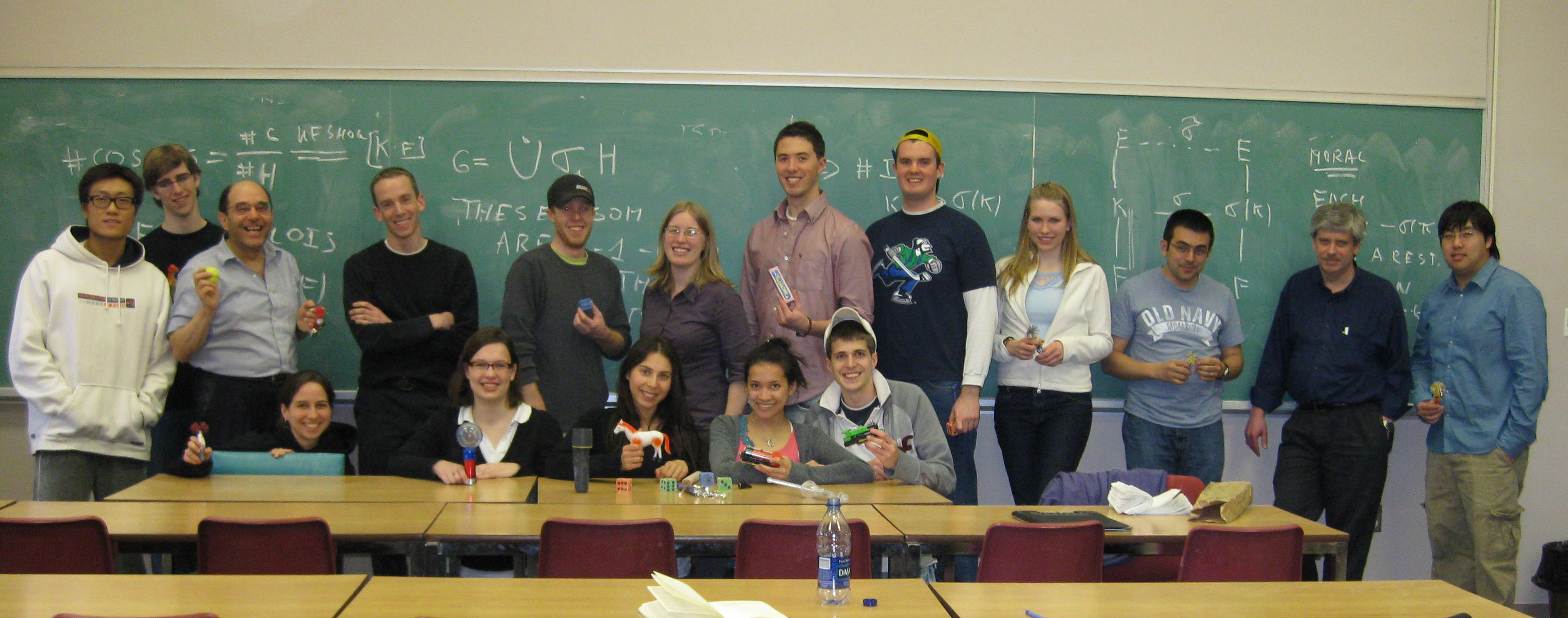 Field Theory Class March 31, 2009
Field Theory Class March 31, 2009
Some of these awesome students from this remarkable class are holding Galois symmetry toys. Galois theory is very deep, beautiful, and important, and at the same time it provides a sandbox where we adult children can play.
RESEARCH HIGHLIGHTS 2020-2022
- Member of Inaugural Class of Fellows, Western Academy for Advanced Research 2022-23, Western University.
- Faculty of Science Distinguished Research Professor 2020-21.
RESEARCH HIGHLIGHTS AND C.V.s
Here is a joint survey paper written with Sunil Chebolu and Dan McQuillan, with illustrations by Matthew Teigen. It was great fun to work on this paper, and we only hoped that it would also be interesting and stimulating for the reader as well. It has been therefore rewarding to receive some very nice responses from our colleagues related to this paper.
Short C.V. (updated August 1, 2024)
THE BRAIN AND MIND INSTITUTE:
Among my most recent interests belongs a strong additional research interest in the application of mathematics to the study of the brain. Fortunately at Western University we have the awesome Brain and Mind Institute. I am very excited about this new direction of my research which seems to have endless possibilities.
CROSS-APPOINTMENT - COMPUTER SCIENCE DEPARTMENT:
I am cross-appointed in the Computer Science Department. Here is a link.
CANADIAN MATHEMATICAL SOCIETY 2019 CLASS OF FELLOWS
(11 mathematicians can make a full soccer team. As a passionate mathematician and soccer player, this makes me very happy!)
WESTERN UNIVERSITY SENATOR (July 2020-July 2024)
Elected to serve in the Western University Senate, beginning July 1, 2020. Served a total of four happy and productive years (elected and re-elected for a total of two terms of two years each) in the Senate and plan to run again for possible re-election to the Senate in early 2026, when I shall be officially eligible to run again.
GALOIS SYMMETRY SCIENCE CENTRE
M. Daley, J. Mináč, L. E. Muller, and B. Wang are beginning to build a Galois symmetry science centre at Western. I plan to expand on this quite soon. Please stay tuned.
TEACHING AWARDS
Canadian Mathematical Society Excellence in Teaching Award 2013
University Students' Council and Alumni Western Teaching Award of Excellence 2009-2010
University Students' Council and Alumni Western Teaching Award of Excellence 1996-1997
UNDERGRADUATE STUDENT RESEARCH AWARD ACTIVITY - SUMMER 2020
I am very pleased to have been a co-supervisor with Lyle E. Muller and Boyu Wang, of four exceptional Summer 2020 applicants for NSERC Undergraduate Student Research Awards. We were very pleased to have been able to plan this work with such gifted and enthusiastic and highly motivated student applicants: Abetare Marevci, Alexandra Busch, Emma Tetelbaum, and Jake Nemiroff. This was a great opportunity and very successful. We continue to be very excited about the possibilities for this joint interdisciplinary research which is being carried out in the Departments of Mathematics, Applied Mathematics, the Brain and Mind Institute, Computer Science, and Physics and Astronomy.
ENCOURAGEMENT FOR APPLICATIONS FOR GRADUATE & POSTGRADUATE STUDY
Three of my PhD students completed their studies in 2019, therefore I am looking for new, enthusiastic and dedicated students. I am also looking for further postdoctoral fellows.
Here at Western University in the Department of Mathematics, we have a wonderful, vital, enthusiastic team that is working feverishly on unveiling some of the exciting secrets of Galois theory and related topics in number theory, algebraic geometry, algebraic topology, analysis and geometry.
The considered topics are fascinating, and they range from classical to the most modern. There is strong collaboration with various mathematicians at Western, as well as worldwide.
POSTDOCTORAL FELLOWS AND RESEARCHERS - 2022 AND BEYOND
Roberto Budzinski (co-supervised with Professor Lyle Muller). Postdoctoral scholar, Department of Mathematics, the Brain and Mind Institute, and the Western Academy for Advanced Research.
Michal Čížek (co-supervised with Professor Lyle Muller). New postdoctoral fellow in the Department of Mathematics and the Western Academy for Advanced Research, Western University (beginning October 1, 2022).
Tung Tho Nguyen (co-supervised with Professor Lyle Muller). Postdoctoral Associate, Department of Mathematics and the Western Academy for Advanced Research, Western University.
Federico W. Pasini (Postdoctoral fellow until June 2022; currently an Assistant Professor, Huron University College, Western University). (2019-20: Federico co-supervised with M. Daley and L. E. Muller, and further consultation with a number of additional great experts. 2020: co-supervised with L. E. Muller and B. Wang, and collaboration with M. Daley.)
Michael Rogelstad - Researcher
CURRENT PHD STUDENTS - 2022 AND BEYOND
Priya Bucha Jain (Western University, co-supervised with Professor Lyle Muller).
Anif Shikder (York University, co-supervised with Professor Lyle Muller)
Esther Yartey (African Institute for Mathematical Sciences, co-supervised with Professor Lyle Muller).
(The work with these awesome students and Professors Christian Maire, Lyle Muller, and others, is extremely exciting and promising in our interdisciplinary group of Galois theory in Mathematics and in Science.)
SUCCESSFUL PHD STUDENT DEFENCE ACTIVITY - SPRING 2019 AND BEYOND
Béatrice Chetard - Postdoctoral Fellow, Stanford University (beginning September 2019). (PhD defence: June 2019; supervised by P. Guillot (University of Strasbourg) and J. Mináč).
Michal Čížek - Postdoctoral Fellow, Western Academy for Advanced Research, Western University (2022-2023). (PhD defence: September 2022; supervised by J. Mináč.)
Oussama Hamza (École normale supérieure de Lyon, co-supervised with Professor Christian Maire and Professor Lyle Muller)
Marina Palaisti - Assistant Professor in Mathematics, Huron University College (January 2018 to present). (PhD defence: March 2019; supervised by J. Mináč.)
SOME FORMER STUDENT ACTIVITY
Daniel McQuillan - Former PhD student and currently Department Chair and Charles A. Dana Professor of Mathematics at Norwich University (since 2017).
CURRENT MASTER'S DEGREE STUDENTS
Jamie Graham (co-supervised with Professor Lyle Muller)
FORMER MASTER'S DEGREE STUDENTS
Alex (Alexandra) Busch (co-supervised with Professor Lyle Muller, Master's degree completed 2022).
Jacqueline Doan (co-supervised with Professor Lyle Muller, Master's degree completed 2022).
Milad Farad (supervised by J. Mináč, Master's degree completed 2019).
TEACHING - FALL 2019
Math 3152A - Combinatorial Mathematics (course outline)
TEACHING - WINTER 2019
Math 3150B - Elementary Number Theory (course outline)
TEACHING - FALL 2018
Math 3121A / 9050A - Advanced Linear Algebra (course outline)
PERSONAL HOMEPAGE (under construction)
RESEARCH
PUBLISHED OR SUBMITTED PAPERS 2015-2019 (for more recent list of publications please see the mathematical archive and MathSciNet):
- 1) P. Guillot, J. Mináč and A. Topaz. Four-fold Massey products in Galois cohomology (with an Appendix by O. Wittenberg). Compositio Math. 154 (2018), no. 9, 1921-1959.
- 2) J. Mináč and N. D. Tân. Triple Massey products and Galois theory. J. Eur. Math. Soc. (JEMS) 19 (2017), no. 1, 255-284.
- 3) J. Mináč and N. D. Tân. Construction of unipotent Galois extensions and Massey products. Adv. Math. 304 (2017), 1021-1054.
- 4) I. Efrat and J. Mináč. Galois groups and cohomological functors. Trans. Amer. Math. Soc. 369 (2017), no. 4, 2697-2720.
- 5) M. Ataei, J. Mináč and N. D. Tân. Description of Galois unipotent extensions. J. Algebra 471 (2017), 193-219.
- 6) J. Mináč and N. D. Tân. Counting Galois U4(Fp)-extensions using Massey products. J. Number Theory 176 (2017), 76-112.
- 7) S. K. Chebolu, D. McQuillan and J. Mináč. Witt's cancellation theorem seen as a cancellation. Expo. Math. 35 (2017), no. 3, 300-314.
- 8) J. Mináč and N. D. Tân. Triple Massey products vanish over all fields. J. Lond. Math. Soc. (2) 94 (2016), no. 3, 909-932.
- 9) S. K. Chebolu, J. Mináč and A. Schultz. Galois p-groups and Galois modules. Rocky Mountain J. Math. 46 (2016), no. 5, 1405-1446.
- 10) J. F. Carlson, S. K. Chebolu and J. Mináč. Ghosts and strong ghosts in the stable category. Canad. Math. Bull. 59 (2016), no. 4, 682-692.
- 11) J. Mináč, M. Rogelstad and N. D. Tân. Dimensions of Zassenhaus filtration subquotients of some pro-p-groups. Israel J. Math. 212 (2016), no. 2, 825-855.
- 12) J. Mináč and N. D. Tân. Triple Massey products over global fields. Doc. Math. 20 (2015), 1467-1480.
- 13) S. K. Chebolu, J. Mináč and C. Quadrelli. Detecting fast solvability of equations via small powerful Galois groups. Trans. Amer. Math. Soc. 367 (2015), no. 12, 8439-8464.
- 14) J. Mináč and N. D. Tân (with an appendix written by I. Efrat, J. Mináč and N. D. Tân). The kernel unipotent conjecture and the vanishing of Massey products for odd rigid fields. Adv. Math. 273 (2015), 242-270.
- 15) P. Guillot and J. Mináč. Extensions of unipotent groups, Massey products and Galois theory. Adv. Math. 354 (2019).
- 16) J. Mináč, F. W. Pasini, C. Quadrelli and N. D. Tân. Koszul algebras and quadratic duals in Galois cohomology (arXiv:1808.01695v1 [math.NT], 5 August, 2018).
- 17) J. Mináč, M. Rogelstad and N. D. Tân. Relations in the maximal pro-p quotients of absolute Galois groups. Trans. Amer. Math. Soc. 373 (2020), no. 4, 2499-2524.
- 18) J. Mináč, M. Palaisti, F. W. Pasini and N. D. Tân. Enhanced Koszul properties in Galois cohomology (arXiv:1811.09272v1 [math.RA]). Research in Math. Sciences, to appear 2020.
RESEARCH AWARDS AND SPECIAL RECOGNITION:
Faculty of Science Distinguished Research Professorships: the first for 2004-2005 and the second for 2020-2021.
Canadian Mathematical Society Summer Meeting 2018, Fredericton, NB. Co-organizer, Special Session: Cohomology - a link between numbers and geometry, June 1-4, 2018.
Banff International Research Station Workshop on Nilpotent Fundamental Groups, June 18 - 23, 2017. Organizers: J. Mináč, F. Pop, A. Topaz and K. G. Wickelgren.
Here is a link to a short video abstract about my paper with Nguyễn Duy Tân, entitled: Counting Galois U4(Fp)-extensions using Massey products, which is published in J. Number Theory (see (6) in the list of 2017 publications above).
Poster for an Algebra Seminar talk delivered, October 18, 2013, related to my joint work with N. D. Tân.
Here is a nice paper entitled: Étude Kummerienne de la q-suite Centrale Descendante d'un Groupe de Galois, by Professor T. Nguyen Quang Do, related to my joint work with S. K. Chebolu, I. Efrat, and M. Spira; as well as to the work of R. Sharifi and others. (Please allow a minute or so to load this document for viewing.) Here is a faster link going directly to this paper.
Here is another nice paper by Professors F. Bogomolov and Y. Tschinkel entitled: Introduction to birational anabelian geometry in Current Developments in Algebraic Geometry (L. Caporaso, J. McKernan, M. Mustata, M. Popa, editors), pages 17-63, MSRI Publications, Volume 59, Cambridge University Press, 2012. (This is a great description of this exciting area, and it includes some of my work with S. K. Chebolu and I. Efrat.)
In the paper, Multiquadratic extensions, rigid fields and Pythagorean fields, D. Leep and T. L. Smith obtained some rather elegant, new proofs of some theorems which I published with A. Adem, W. Gao and D. Karagueuzian in 2001; and also with T. L. Smith in 2000.
Some more papers related to my research may be found here. (See MathSciNet for a comprehensive list of my publications.)
SELECTED INVITED ADDRESSES AND SCHOLARLY ACTIVITIES:
- Co-organizer, Special Session: Groups and their cohomological invariants in Arithmetic and Geometry, American Mathematical Society Sectional Meeting, University of Texas at El Paso, September 12-13, 2020. Organized by S. Gille and N. Karpenko (both University of Alberta) and J. Mináč (Western University).
- Invited plenary speaker, Centro Internazionale per la Ricerca Matematica (CIRM) conference: “New Trends Around Profinite Groups,” Levico Terme, Trentino, Italy, September 14-18, 2020. Organized by Eloisa Detomi (Università di Padova), Benjamin Klopsch (Universitaet Duesseldorf), Peter Symonds (University of Manchester), Christopher Voll (Universitaet Bielefeld), and Thomas Weigel (Università di Milano Bicocca).
- Invited lecture, Number Theory Seminar, Department of Mathematics, Cornell University, Ithaca, New York, May 1, 2020.
- Invited Colloquium Speaker, Pure Mathematics Colloquium, University of Waterloo, April 1, 2019.
- Co-organizer, Special Session, Canadian Mathematical Society Summer Meeting, Fredericton, New Brunswick, June 1-4, 2018. (Organized by S. Gille, J. Mináč and K. Zaynullin.)
- Co-organizer, Banff International Research Station Workshop: Nilpotent Fundamental Groups, June 18-23, 2017. (Organized by J. Mináč, F. Pop, A. Topaz and K. G. Wickelgren.)
- 2015 American Mathematical Society Fall Eastern Sectional Meeting, Rutgers University.
- Workshop on Number Theory with a view towards Transcendence and Diophantine Approximation, University of Ottawa, June 8-10, 2013. Sponsored by the Fields Institute and organized by Damien Roy, University of Ottawa, and Cameron Stewart, University of Waterloo.
- 70th Algebra Days, Carleton University, October 20-21, 2012. (Sponsored by the Fields Institute, the Ottawa-Carleton Institute for Algebra and Number Theory, and the School of Mathematics and Statistics, Carleton University.)
- IBG Advanced International School on Galois Groups, Bilbao, Spain, July 2012.
SPECIALIZATIONS:
Algebraic Number Theory, Galois Cohomology, Quadratic Forms, Field Theory, Brauer Groups, Algebraic K-Theory, Algebraic Geometry, and Algebraic Topology.
RESEARCH INTERESTS:
The Bloch-Kato conjecture, quadratic forms, Galois groups and Galois cohomology, Grothendieck's anabelian geometry, zeta functions, analytic pro-p groups, algebraic K-theory, cohomology of finite p-groups, Galois groups of maximal p-extensions with a given set of ramification points, the stable homotopy category, and Freyd's generating hypothesis. I am also very interested in both the finite generation of Tate cohomology and Lie algebras associated with Galois groups.
I am also interested in Massey products, formality-like properties and Koszul properties of Galois cohomology, arithmetic geometry, Hodge theory, the section conjecture, the Langlands program, motivic cohomology, pefectoids, moduli spaces, Galois modules, and representation theory.
Recently I began together with my collaborators to investigate some novel approaches of mathematics to medicine.
PUBLICATIONS
(For some possible updates to my list of publications, please see my C. V. above.) Here are two more links to arXiv.org: (1) and (2).
RESEARCH AND M.S.R.I.
Here are some cool and interesting survey papers on some elementary aspects of the values of the zeta function, where the authors also refer to my observation (A Remark on the Values of the Zeta Function, Expo. Math. 12 (1994), 459-462):
- Bernoulli Numbers and the Riemann Zeta Function, by B. Sury.
- The Continuing Story of Zeta, by G. Everest, Ch. Röttger and T. Ward.

Artist: Nikita Maria Findlay
CURRENT AND RECENTLY SUPERVISED POSTDOCTORAL FELLOWS, VISITING PROFESSORS AND INTERNATIONAL STUDENTS (INCLUDING POSSIBILITIES IN THE NEAR FUTURE)
- Ronie Peterson Dario (September 2018 - June 2019, visiting professor)
- Christian Maire (Winter 2020)
- Hamza Oussama (École normale supérieure de Lyon student co-supervised with Ch. Maire, 2019-2020)
- Federico W. Pasini (July 2017 - July 2019, supervised by J. Mináč). August 2019 - 2020, Federico Pasini's current new interdisciplinary projects have attracted some broad supervision support across Western's community of researchers. Federico's main supervisors are: M. Daley, J. Mináč and L. Muller. His further co-supervisors and consultants are T. Barron, Ch. Hall, D. Jeffrey, R. Valluri, B. Wang and G. Wild.
- Michael Rogelstad (September 2017 - present)
- Nguyen Duy Tân (July 2018 - August 2018 and July 2015 - August 2015)
- Nguyen Tho Xuan (Currently working at the University of Hanoi, Vietnam. We hope that Tho will soon be able to join our team here. Here is a link to Tho's homepage at Arizona State University where he completed his PhD studies in the spring of 2019.)
CURRENT AND RECENTLY COMPLETED DOCTORAL STUDENT SUPERVISION
- Ali Alkhairy
- Béatrice Chetard (PhD completed, spring 2019 (co-supervised with P. Guillot - University of Strasbourg), postdoctoral fellowship beginning at Stanford University, September 2019)
- Michal Čížek
- Marina Palaisti (PhD completed, spring 2019, with permanent position obtained as an Assistant Professor at Huron University College, spring 2019)
CURRENT MASTER'S STUDENT SUPERVISION
- Priya Bucha Jain (I am very happy and excited about my new master's student who is beginning studies with me this September 2019.)
- Milad Fakhari (2018 - present / co-supervised with D. Riley)

MATH CLUB AT WESTERN (MaCAW)
Here above is a link to MaCAW with some awesome graduate students with some great enthusiasm, excitement, and always interesting activities. I feel very privileged to work with some of them closely.
FILM / MATHEMATICS / THE ARTS
- Here is a link to a short video abstract about my paper with Nguyễn Duy Tân, entitled: Counting Galois U4(Fp)-extensions using Massey products, which is published in the Journal of Number Theory (see (6) in the list of 2017 publications above).
- Here is a link to one of my mathematical theatrical lectures delivered in my course on Elementary Number Theory, with some special connections to the timeless tale of Romeo and Juliet.
- Here is a link from IMDb to my work in the film industry. Here is a second link to IMDb with my photograph. We hope to eventually merge these two pages into one page on IMDb.
- Here is a link to my brother, Matej Mináč, a documentary filmmaker with whom I also work.

With Vaclav Havel (former President of the Czech Republic) at the 2006 Karlovy Vary International Film Festival.

With Nastassja Kinski at the Karlovy Vary International Film Festival.

PUBLISH OR PERISH! This is a reconstruction of the closing scene from a mathematical theatrical lecture, Hamlet and Pfister Forms, performed at the mathematical institute in Oberwolfach, Germany, 1992 (Ján Mináč and Leslie Hallock).
SOME MEDIA LINKS
Here is a 2025 Western News article by Keri Ferguson, concerning the nice surprise shown at the top of this homepage.
Here is a link to a 2019 Western News article by author Debora Van Brenk, about a happy mathematician seeking solutions in symmetry.
Here is a link to a Western News page with "News and Notes".
Here is a link to a Western News page by various authors, about "Science Honours its Own".
Here is a link to a Western News page about the University Students' Council awards honouring teachers and students.
Here is a link to a Western News article by author Jason Winders, about the Canadian Mathematical Society 2013 Excellence in Teaching Award.
Here is a link to a 2013 media release from the Canadian Mathematical Society about the teaching award mentioned above.



