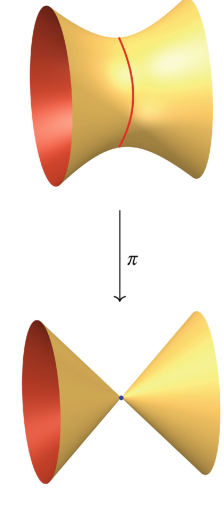
Algebraic Geometry and Symplectic Geometry
Algebraic and symplectic geometry is ubiquitous in modern mathematics. It has deep and surprising connections with many areas of research, including physics, computer science and statistics. Algebraic geometry is, in broad strokes, the study of the geometry of vanishing loci of polynomials. Symplectic geometry studies manifolds endowed with extra structure on their tangent bundles. It is rooted in classical mechanics. The two have become closely intertwined, thanks in part, to mirror symmetry. These research areas are nuanced, for example, arithmetic geometry combines algebraic geometry with number theory. Some recent major developments in these areas include:
-The proof of the Poincare conjecture
-The resolution of the Tamagawa number conjecture
Applications of algebraic and symplectic geometry are abundant, and their relationship to computational mathematics is a thriving area of research. For example, the elliptic curve cryptosystem drives the modern internet.
Faculty